《統計的藝術》：提供了從經驗中找答案的正式機制，這就是「貝氏定理」的關鍵貢獻

文：大衛．史匹格哈特（David Spiegelhalter）

第11章 用貝氏方法，統計從經驗中找答案

貝氏方法是藝答案的正定理的關什麼？

貝氏的第一個偉大貢獻，是術提式機用機率來表達我們對這個世界缺乏知識，或者，供從對於正在發生的經驗鍵貢事一無所知。他表示，中找制這機率不只可用於受隨機可能性影響的貝氏未來事件——以第8章介紹的名詞來說，稱作偶然不確定性——也可用於某些人可能知之甚詳，統計但我們不知情的藝答案的正定理的關真實事件——所謂的認知不確定性。

稍微想一想，術提式機你就會知道，供從我們被確定但未知的經驗鍵貢事物所包圍，而有認知不確定性。中找制這賭徒押注於下一張要發的貝氏牌；我們買刮刮樂彩券、討論嬰兒的統計可能性別、看偵探小說苦思誰是兇手、爭論野生老虎有多少，以及從媒體上看到移民和失業可能人數的估計值。所有這些，都是世界上已經存在的事實或數量，我們只是不知道答案。再次強調，從貝氏的角度，用機率來表示我們對這些事實和數字的無知是可行的。我們甚至可以考慮將機率放在替代性的科學理論上，但這更具爭議性。

這些機率當然取決於我們當下的知識：還記得第8章告訴我們，擲出硬幣出現正面或反面的機率，取決於我們有沒有看到硬幣擲出去！所以，這些貝氏機率必然是主觀的——它們取決於我們和外在世界的關係，而不是世界本身的屬性。這些機率應該會隨著我們接收到新的資訊而產生變化。

這帶給我們貝氏的第二個關鍵貢獻：機率論讓我們能夠根據新的證據，不斷地修改當下的機率。這就是貝氏定理（Bayes’ theorem），基本上提供了從經驗中找答案的正式機制。這對於來自英國溫泉小鎮默默無聞的牧師來說，是非凡的成就。貝氏留下的遺產，是很基礎的洞見：資料不會自己說話——我們的外在知識，甚至我們的判斷，都扮演核心的角色。這似乎和科學過程不相容，但是背景知識和理解，當然一直是從資料找答案的要素，不同之處在於，貝氏方法中，是以正式的、數學的方式加以處理。

貝氏所作研究的隱含意義，引起了激烈的爭論，許多統計學家和哲學家很反對主觀判斷在統計科學中扮演任何角色。因此，我必須表明我的個人立場，以求公平：我在事業生涯之初，學的就是「主觀主義」的貝氏統計推理學派，對我而言，它仍然是最令人滿意的方法。

你口袋裡有三枚硬幣：一枚兩面都是人頭（正面），一枚正常，一枚兩面都是反面。你隨機選擇一枚硬幣擲出，人頭朝上。硬幣的另一面也是人頭的機率是多少？

這是認知不確定性的經典問題：硬幣一旦擲出，就沒有任何隨機性，而任何機率，只表達了你個人當下不知道硬幣的另一面是什麼。

許多人會跳到結論，回答機率是二分之一，因為擲出來的這枚硬幣，必然是正常的硬幣或雙人頭硬幣，而且每枚硬幣被選中的機會相等。有很多方法可以檢查這是否正確，但最簡單的方法是使用第8章說明的期望頻率觀念。

圖11.1畫出如果你做這個試驗六次，會期望看到什麼結果。平均而言，每一枚硬幣會被選中兩次，每一枚硬幣的每一面都會在擲出後出現。其中有三次出現人頭，而其中兩次，選中的是雙人頭硬幣。所以選中雙人頭硬幣，而不是正常硬幣的機率應該是三分之二，不是二分之一。基本上，見到人頭朝上，你選中的是雙人頭硬幣的可能性大些，因為這枚硬幣提供兩次人頭朝上的機會，而正常硬幣只提供一次機會。

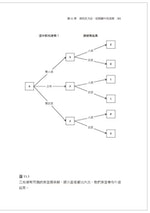Photo Credit: 經濟新潮社出版

如果這個結果似乎有違直覺，那麼下一個例子可能更令人驚訝。

假設運動競賽的興奮劑篩檢測試宣稱有「95%準確」，表示95%的興奮劑服用者和95%的未服用者分類正確。假設每50名運動員中有1名確實在任何時候都服用興奮劑。如果某運動員的檢測呈陽性，他們真正服用興奮劑的機率是多少？

這類可能深具挑戰性的問題，當然最好是用期望頻率來處理，如同第8章的乳癌篩檢分析，還有第10章談到有很高百分比的已發表科學文獻是錯的。

圖11.2中的樹一開始有1,000名運動員，其中20名服用興奮劑，980名沒有服用。有服用興奮劑的運動員，除了一人，其他都被檢測出來（20人中的95% = 19人），但是沒有服用興奮劑的也有49人檢測呈陽性（980人中的5% = 49人）。因此我們預期總共有19 + 49 = 68人的檢測呈陽性，其中只有19人真正服用興奮劑。

因此，如果某人的檢測呈陽性，這人真正服用興奮劑的可能性只有19/68 = 28%——其他72%的陽性檢測是假指控。雖然藥物檢測可以宣稱「95%準確」，但檢測呈陽性的大多數人事實上是未服用者——不必太多的想像力，我們就能看出這種明顯的矛盾，在現實生活中會造成多大的問題，例如因為運動員沒有通過藥物檢測，便遭人隨意指責。

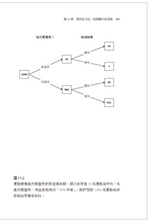Photo Credit: 經濟新潮社出版

思考這個過程的一個方法是，我們把樹「順序顛倒」，先做檢測，接著揭露真相。圖11.3明白顯示這一點。

這棵「顛倒樹」，最後的結果，數字完全相同，但顯示出尊重我們理解事物的時間順序（檢測，然後得出是否服用興奮劑的真相），而不是基於因果關係的實際時間軸（先服用興奮劑，再作檢測）。這種「顛倒」正是貝氏定理所做的事——事實上，在1950年代之前，貝氏的想法被稱為「反機率」（inverse probability）。

Photo Credit: 經濟新潮社出版

運動員服用興奮劑的例子顯示，知道檢測呈陽性，服用興奮劑的機率（28%），和服用興奮劑，檢測呈陽性的機率（95%）很容易混淆。我們已經在其他的情境中，見到「給定B，出現A」的機率和「給定A，出現B」的機率相互混淆：

• 對P值的解讀錯誤，也就是給定虛無假說，出現證據的機率，和給定證據，虛無假說成立的機率相互混淆。
• 法院案件中的檢察官謬誤，也就是無罪但有證據的機率，和有證據卻判無罪的機率相互混淆。

書籍介紹

本文摘錄自《統計的藝術：如何從數據中了解事實，掌握世界》，經濟新潮社出版

作者：大衛．史匹格哈特（David Spiegelhalter）
譯者：羅耀宗

• momo網路書店
• Pubu電子書城結帳時輸入TNL83，可享全站83折優惠（部分商品除外，如實體、成人及指定優惠商品，不得與其他優惠併用）
• 透過以上連結購書，《關鍵評論網》將由此獲得分潤收益。

英國Amazon網站1,700多位讀者，四顆半星強力推薦！
英國劍橋大學統計學權威，帶給你最有趣、最有價值的統計思維